Fork me on GitHub

排序算法

发表于 | 分类于 | 阅读次数： | 本文字数： 17k | 阅读时长 ≈ 0:28

选择排序（Selection Sort）

选择排序算法通过重复查找未排序部分的最小元素（考虑升序）并将其放在开头来排序数组。算法在给定数组中维护两个子数组。

  • 已经排序好的子数组
  • 剩下未排序的子数组

在选择排序的每一次迭代中，挑选未排序子数组中的最小元素（考虑升序），并将其移至排序后的子数组中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// Java program for implementation of Selection Sort
class SelectionSort
{
    void sort(int arr[])
    {
        int n = arr.length;
 
        // One by one move boundary of unsorted subarray
        for (int i = 0; i < n-1; i++)
        {
            // Find the minimum element in unsorted array
            int min_idx = i;
            for (int j = i+1; j < n; j++)
                if (arr[j] < arr[min_idx])
                    min_idx = j;
 
            // Swap the found minimum element with the first element
            int temp = arr[min_idx];
            arr[min_idx] = arr[i];
            arr[i] = temp;
        }
    }
 
    // Prints the array
    void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i]+" ");
        System.out.println();
    }
 
    // Driver code to test above
    public static void main(String args[])
    {
        SelectionSort ob = new SelectionSort();
        int arr[] = {64,25,12,22,11};
        ob.sort(arr);
        System.out.println("Sorted array");
        ob.printArray(arr);
    }
}

时间复杂度：O(n2)O\left( n^{2}\right)

冒泡排序（Bubble Sort）

冒泡排序通过反复交换相邻元素（如果顺序错误）来工作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// Java program for implementation of Bubble Sort
class BubbleSort
{
    void bubbleSort(int arr[])
    {
        int n = arr.length;
        for (int i = 0; i < n-1; i++)
            for (int j = 0; j < n-i-1; j++)
                if (arr[j] > arr[j+1])
                {
                    // swap temp and arr[i]
                    int temp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = temp;
                }
    }
 
    /* Prints the array */
    void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
    // Driver method to test above
    public static void main(String args[])
    {
        BubbleSort ob = new BubbleSort();
        int arr[] = {64, 34, 25, 12, 22, 11, 90};
        ob.bubbleSort(arr);
        System.out.println("Sorted array");
        ob.printArray(arr);
    }
}

优化实现： 即使数组已经有序，上述函数也会运行O(n2)O\left( n^{2}\right)时间。如果内部循环没有引起任何交换，可以通过停止算法来优化它。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// Optimized java implementation of Bubble sort 
class GFG 
{
    // An optimized version of Bubble Sort
    static void bubbleSort(int arr[], int n)
    {
        int i, j, temp;
        boolean swapped;
        for (i = 0; i < n - 1; i++) 
        {
            swapped = false;
            for (j = 0; j < n - i - 1; j++) 
            {
                if (arr[j] > arr[j + 1]) 
                {
                    // swap arr[j] and arr[j+1]
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    swapped = true;
                }
            }
 
            // IF no two elements were 
            // swapped by inner loop, then break
            if (swapped == false)
                break;
        }
    }
 
    // Function to print an array 
    static void printArray(int arr[], int size)
    {
        int i;
        for (i = 0; i < size; i++)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
    // Driver program
    public static void main(String args[])
    {
        int arr[] = { 64, 34, 25, 12, 22, 11, 90 };
        int n = arr.length;
        bubbleSort(arr, n);
        System.out.println("Sorted array: ");
        printArray(arr, n);
    }
}

时间复杂度：O(n2)O\left( n^{2}\right)

插入排序（Insertion Sort）

1
2
3
4
// Sort an arr[] of size n
insertionSort(arr, n)
Loop from i = 1 to n-1.
……a) Pick element arr[i] and insert it into sorted sequence arr[0…i-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
// Java program for implementation of Insertion Sort
class InsertionSort
{
    /*Function to sort array using insertion sort*/
    void sort(int arr[])
    {
        int n = arr.length;
        for (int i=1; i<n; ++i)
        {
            int key = arr[i];
            int j = i-1;
 
            /* Move elements of arr[0..i-1], that are
               greater than key, to one position ahead
               of their current position */
            while (j>=0 && arr[j] > key)
            {
                arr[j+1] = arr[j];
                j = j-1;
            }
            arr[j+1] = key;
        }
    }
 
    /* A utility function to print array of size n*/
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i] + " ");
 
        System.out.println();
    }
 
    // Driver method
    public static void main(String args[])
    {        
        int arr[] = {12, 11, 13, 5, 6};
 
        InsertionSort ob = new InsertionSort();        
        ob.sort(arr);
         
        printArray(arr);
    }
}

时间复杂度：O(n2)O\left( n^{2}\right)

链表的插入排序

1
2
3
4
1) Create an empty sorted (or result) list
2) Traverse the given list, do following for every node.
......a) Insert current node in sorted way in sorted or result list.
3) Change head of given linked list to head of sorted (or result) list.

归并排序（Merge Sort）——分治思想

1
2
3
4
5
6
7
8
9
10
MergeSort(arr[], l,  r)
If r > l
     1. Find the middle point to divide the array into two halves:  
             middle m = (l+r)/2
     2. Call mergeSort for first half:   
             Call mergeSort(arr, l, m)
     3. Call mergeSort for second half:
             Call mergeSort(arr, m+1, r)
     4. Merge the two halves sorted in step 2 and 3:
             Call merge(arr, l, m, r)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
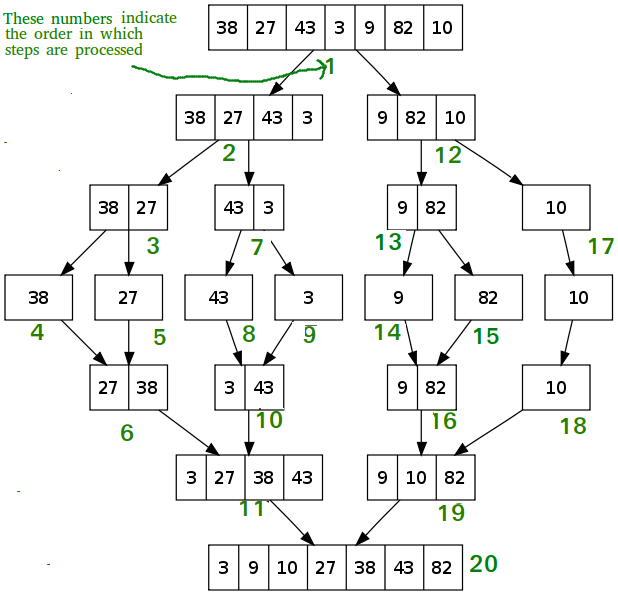
/* Java program for Merge Sort */
class MergeSort
{
    // Merges two subarrays of arr[].
    // First subarray is arr[l..m]
    // Second subarray is arr[m+1..r]
    void merge(int arr[], int l, int m, int r)
    {
        int[] tmp = new int[r - l + 1];
        int i = l, j = m, k = 0;
        while (i < m && j <= r) {
            if (arr[i] <= arr[j]) {
                tmp[k] = arr[i];
                k++;
                i++;
            } else {
                tmp[k] = arr[j];
                j++;
                k++;
            }
        }
        while (i < m) {
            tmp[k] = arr[i];
            i++;
            k++;
        }
        while (j <= r) {
            tmp[k] = arr[j];
            j++;
            k++;
        }
   }
 
    // Main function that sorts arr[l..r] using
    // merge()
    void sort(int arr[], int l, int r)
    {
        if (l < r)
        {
            // Find the middle point
            int m = (l+r)/2;
 
            // Sort first and second halves
            sort(arr, l, m);
            sort(arr , m+1, r);
 
            // Merge the sorted halves
            merge(arr, l, m, r);
        }
    }
 
    /* A utility function to print array of size n */
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i] + " ");
        System.out.println();
    }
 
    // Driver method
    public static void main(String args[])
    {
        int arr[] = {12, 11, 13, 5, 6, 7};
 
        System.out.println("Given Array");
        printArray(arr);
 
        MergeSort ob = new MergeSort();
        ob.sort(arr, 0, arr.length-1);
 
        System.out.println("\nSorted array");
        printArray(arr);
    }
}

时间复杂度：O(nlog⁡n)O\left( n\log n\right)

链表的归并排序

1
2
3
4
5
6
7
8
9
10
MergeSort(headRef)
1) If head is NULL or there is only one element in the Linked List 
    then return.
2) Else divide the linked list into two halves.  
      FrontBackSplit(head, &a, &b); /* a and b are two halves */
3) Sort the two halves a and b.
      MergeSort(a);
      MergeSort(b);
4) Merge the sorted a and b and update the head pointer using headRef.
     *headRef = SortedMerge(a, b);

一下代码巧妙的使用两个指针移动来寻找中间节点，第一个指针每次移动一格，第二个指针每次移动两格，当第二个指针到达末尾时，第一个指针恰好到达中点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
// Java program to illustrate merge sorted
// of linkedList
 
public class linkedList 
{
    node head = null;
    // node a,b;
    static class node 
    {
        int val;
        node next;
 
        public node(int val) 
        {
            this.val = val;
        }
    }
     
    node sortedMerge(node a, node b) 
    {
        node result = null;
        /* Base cases */
        if (a == null)
            return b;
        if (b == null)
            return a;
 
        /* Pick either a or b, and recur */
        if (a.val <= b.val) 
        {
            result = a;
            result.next = sortedMerge(a.next, b);
        } 
        else
        {
            result = b;
            result.next = sortedMerge(a, b.next);
        }
        return result;
 
    }
 
    node mergeSort(node h) 
    {
        // Base case : if head is null
        if (h == null || h.next == null)
        {
            return h;
        }
 
        // get the middle of the list
        node middle = getMiddle(h);
        node nextofmiddle = middle.next;
 
        // set the next of middle node to null
        middle.next = null;
 
        // Apply mergeSort on left list
        node left = mergeSort(h);
 
        // Apply mergeSort on right list
        node right = mergeSort(nextofmiddle);
 
        // Merge the left and right lists
        node sortedlist = sortedMerge(left, right);
        return sortedlist;
    }
 
    // Utility function to get the middle of the linked list
    node getMiddle(node h) 
    {
        //Base case
        if (h == null)
            return h;
        node fastptr = h.next;
        node slowptr = h;
         
        // Move fastptr by two and slow ptr by one
        // Finally slowptr will point to middle node
        while (fastptr != null)
        {
            fastptr = fastptr.next;
            if(fastptr!=null)
            {
                slowptr = slowptr.next;
                fastptr=fastptr.next;
            }
        }
        return slowptr;
    }
 
    void push(int new_data) 
    {
        /* allocate node */
        node new_node = new node(new_data);
 
        /* link the old list off the new node */
        new_node.next = head;
 
        /* move the head to point to the new node */
        head = new_node;
    }
 
    // Utility function to print the linked list
    void printList(node headref) 
    {
        while (headref != null) 
        {
            System.out.print(headref.val + " ");
            headref = headref.next;
        }
    }
     
    public static void main(String[] args) 
    {
 
        linkedList li = new linkedList();
        /*
         * Let us create a unsorted linked lists to test the functions Created
         * lists shall be a: 2->3->20->5->10->15
         */
        li.push(15);
        li.push(10);
        li.push(5);
        li.push(20);
        li.push(3);
        li.push(2);
        System.out.println("Linked List without sorting is :");
        li.printList(li.head);
 
        // Apply merge Sort
        li.head = li.mergeSort(li.head);
        System.out.print("\n Sorted Linked List is: \n");
        li.printList(li.head);
    }
}

堆排序（Heap Sort）

堆排序是基于Binary Heap数据结构的基于比较的排序算法。它类似于我们首先找到最大元素然后和最后位置交换的选择排序。我们对剩下的元素重复相同的过程。

什么是Binary Heap

Binary Heap是一个完整二叉树，其中项以特殊顺序存储，使得父节点中的值比其两个子节点中的值更大（或更小）。前者称为最大堆，后者称为最小堆。堆可以用二叉树或数组表示。

用数组表示Binary Heap，如果父节点存储在索引i处，则左边的孩子索引为2 * i + 1，右边的孩子索引为2 * i + 2（假设索引从0开始）。

按升序排序的堆排序算法：

  • 根据输入数据构建一个最大堆。
  • 此时，最大的元素存储在堆的根。将它和堆的最后一项交换，然后将堆的大小减1。最后，heapify树的根。
  • 在堆大小大于1的情况下重复上述步骤。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
// Java program for implementation of Heap Sort
public class HeapSort
{
    public void sort(int arr[])
    {
        int n = arr.length;
 
        // Build heap (rearrange array)
        for (int i = n / 2 - 1; i >= 0; i--)
            heapify(arr, n, i);
 
        // One by one extract an element from heap
        for (int i=n-1; i>=0; i--)
        {
            // Move current root to end
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
 
            // call max heapify on the reduced heap
            heapify(arr, i, 0);
        }
    }
 
    // To heapify a subtree rooted with node i which is
    // an index in arr[]. n is size of heap
    void heapify(int arr[], int n, int i)
    {
        int largest = i;  // Initialize largest as root
        int l = 2*i + 1;  // left = 2*i + 1
        int r = 2*i + 2;  // right = 2*i + 2
 
        // If left child is larger than root
        if (l < n && arr[l] > arr[largest])
            largest = l;
 
        // If right child is larger than largest so far
        if (r < n && arr[r] > arr[largest])
            largest = r;
 
        // If largest is not root
        if (largest != i)
        {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;
 
            // Recursively heapify the affected sub-tree
            heapify(arr, n, largest);
        }
    }
 
    /* A utility function to print array of size n */
    static void printArray(int arr[])
    {
        int n = arr.length;
        for (int i=0; i<n; ++i)
            System.out.print(arr[i]+" ");
        System.out.println();
    }
 
    // Driver program
    public static void main(String args[])
    {
        int arr[] = {12, 11, 13, 5, 6, 7};
        int n = arr.length;
 
        HeapSort ob = new HeapSort();
        ob.sort(arr);
 
        System.out.println("Sorted array is");
        printArray(arr);
    }
}

时间复杂度：O(nlog⁡n)O\left( n\log n\right)

堆排序的应用

  • 对几乎排好序的（或K个排好序的）数组进行排序。
  • 求数组中的k个最大（或最小）元素。

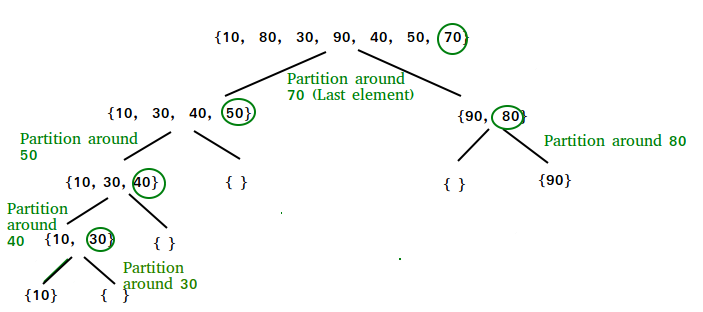
快速排序（QuickSort）——分治思想

快排选择一个元素作为枢轴（pivot），并将给定的数组根据选取的枢轴分区。有许多选择枢轴不同的方式。

  • 始终选择第一个元素作为枢轴。
  • 总是选择最后一个元素作为枢轴。
  • 选择一个随机元素作为枢轴。
  • 选择中位数为枢轴。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public static void quickSort(int[] arr){
    qsort(arr, 0, arr.length-1);
}
private static void qsort(int[] arr, int low, int high){
    if (low < high){
        int pivot=partition(arr, low, high);        //将数组分为两部分
        qsort(arr, low, pivot-1);                   //递归排序左子数组
        qsort(arr, pivot+1, high);                  //递归排序右子数组
    }
}
private static int partition(int[] arr, int low, int high){
    int pivot = arr[low];     //枢轴记录
    while (low<high){
        while (low<high && arr[high]>=pivot) --high;
        arr[low]=arr[high];             //交换比枢轴小的记录到左端
        while (low<high && arr[low]<=pivot) ++low;
        arr[high] = arr[low];           //交换比枢轴小的记录到右端
    }
    //扫描完成，枢轴到位
    arr[low] = pivot;
    //返回的是枢轴的位置
    return low;
}

时间复杂度：O(nlog⁡n)O\left( n\log n\right)

当最左元素或者最右元素被选为枢轴时，最坏情况发生在以下情形：

  • 数组已经是相同的顺序。
  • 数组已经是相反的顺序。
  • 所有元素都相等。

所以尽量选择随机元素或者中间的元素或者中位数作为枢轴来避免最坏情况。

Shell Sort（希尔排序）

希尔排序基本思想为在直接插入排序的思想下设置一个最小增量dk,刚开始dk设置为n/2。进行插入排序，随后再让dk=dk/2,再进行插入排序，直到dk为1时完成最后一次插入排序，此时数组完成排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public static void shell_sort(int array[],int lenth){

   int temp = 0;
   int incre = lenth;

   while(true){
       incre = incre/2;

       for(int k = 0;k<incre;k++){    //根据增量分为若干子序列

           for(int i=k+incre;i<lenth;i+=incre){

               for(int j=i;j>k;j-=incre){
                   if(array[j]<array[j-incre]){
                       temp = array[j-incre];
                       array[j-incre] = array[j];
                       array[j] = temp;
                   }else{
                       break;
                   }
               }
           }
       }

       if(incre == 1){
           break;
       }
   }
}

最坏时间复杂度为O(n2)O\left( n^{2}\right)；最优时间复杂度为O(n)O\left( n\right)；平均时间复杂度为O(n1.3)O\left( n^{1.3}\right)。辅助空间O(1)O\left(1\right)。稳定性：不稳定。希尔排序的时间复杂度与选取的增量有关，选取合适的增量可减少时间复杂度。

求鼓励，求支持！